Methods

Why are some countries rich and others poor? For centuries, scholars have been working to identify the factors that explain differences in prosperity. Their work has taught us about the importance of institutions^1–3, technology^4,5, human capital, and social capital^6–9.Yet, we have also learned that economic prosperity cannot be tied narrowly to single factors. In fact, differences between rich and poor countries are multifarious, and include numerous highly specific factors^10,11. Hence, we need ways to capture international differences in development outcomes that are not narrowly focused on a single factor, but that consider “all of the above.”

Economic complexity can help us understand the development of national and regional economies through measures focused on “all of the above.” Its methods use high resolution data on the activities that are present in locations to predict the development dynamics of countries, cities, and regions. These methods can predict the economic activities that a country, city, or region will enter or exit in the future^12,13, as well as an economy's expected level of income^14,15, economic growth^14,15, income inequality¹⁶, and emissions^17,18.

In this section, we explain some of the basic ideas that shape the field of Economic Complexity.

Economic Complexity is both an academic field and a concept.

As an academic field, Economic Complexity studies the geography and dynamics of economic activities using methods inspired in ideas from complex systems, networks, and computer science.

That makes the field of Economic Complexity somehow unique, is that it studies the geography of activities using an outcomes based approach. That is, instead of trying to figure out what capabilities or factors drive an economy, it uses data on the geography of economic activities to infer the presence of bundles of capabilities.

Economic complexity methods are used to predict and explain the dynamics of economic activities and of economic aggregates, such as income per capita. For example, using the concept of relatedness (e.g. the product space), one can take data on the products that a country exports, or the industries present in a city, and predict which products or industries are more likely to grow in the future^11,12.What is good about these methods is that they do not make any strong assumptions about the capabilities or factors required to produce each product because they leverage the idea that similar economic activities require similar capabilities (without having to identify what these capabilities are).

Similarly, metrics of Economic Complexity, such as the Economic Complexity Index, can be used to predict a country's expected level of income^13,14,economic growth^13,14, income inequality¹⁵,and greenhouse gas emissions^16,17. Measures of the complexity required to produce an activity also help explain the spatial concentration of economic activities (complex economic activities are more concentrated in space)¹⁸.

The field of Economic Complexity is closely related to other fields of study, such as Economic Geography, which has long focused on the geographic distribution of economic activity, and Network Science, since Economic Complexity uses methods developed originally in the Network Science and Complex Systems community.

As a concept, Economic Complexity is related to the idea of the division of labor, or more specifically, the division of knowledge. Because individuals are limited in what they can know^15,19,the only way economies can expand their knowledge is by dividing it up among many individuals. Complex products, like medical imaging devices or jet engines, require vast amounts of knowledge that can only be accumulated in large networks of people.

The accumulation of knowledge in large professional networks is only possible in economies with good institutions, social capital, infrastructure, and education¹⁹.This adds credence to the idea that economic complexity measures gather evidence on “all of the above”.

Outside academia, Economic Complexity methods are used by multilateral organizations and national development agencies focused on economic development, by export promotion agencies and shipping companies wanting to predict the evolution of international trade patterns, and by financial companies (to price bonds and other instruments, because of the ability of economic complexity to predict long term economic growth).

Relatedness measures the “similarity” or “compatibility” between an economy and an activity. For instance, it can be used to estimate whether the export structure of Bulgaria is compatible with what is needed to export cars, or if the technologies in which Toulouse has patented in the past are compatible with patenting in a particular technology, such as liquid crystal displays. Relatedness can be used to predict the probability that a location will enter or exit an activity.

Usually, scholars measure relatedness between a location and an economic activity to predict the probability that a region will enter or exit that activity in the future. The fact that the growth of an activity in a location is correlated with relatedness is known as The Principe of Relatedness¹³: a statistical law that tells us that the probability that a location (a country, city, or region), enters an economic activity (e.g. a product, industry, technology), grows with the number of related activities present in a location. The principle of relatedness has been shown to be true for countries entering new products^12,15,regions entering new industries^20,21, cities patenting in new technologies,7^22,23,and even universities publishing in new research areas²⁴.

Relatedness is usually calculated by looking at the percentage of related activities that are present in a location. Formally, let \(M_{cp}\) be a matrix indicating the presence of activity p in location c , and let \(\phi_{pp'}\) be a measure of similarity, or proximity, between activities \(p\) and \(p'\) . Then, we can estimate the relatedness w between location c and activity p as:

Similarly, we can estimate relatedness by looking at similar locations instead of similar activities.

Where \(\phi_{cc'}\) is a matrix of similarity between locations c and c' .

Similarity metrics, such as \(\phi_{pp'}\) , are known as metrics of proximity. There are multiple ways to estimate proximity, using simple indicators such as conditional probabilities¹²,or more sophisticated indicators,such as the ratio between observed coincidences and those expected from an econometric model.^20,21

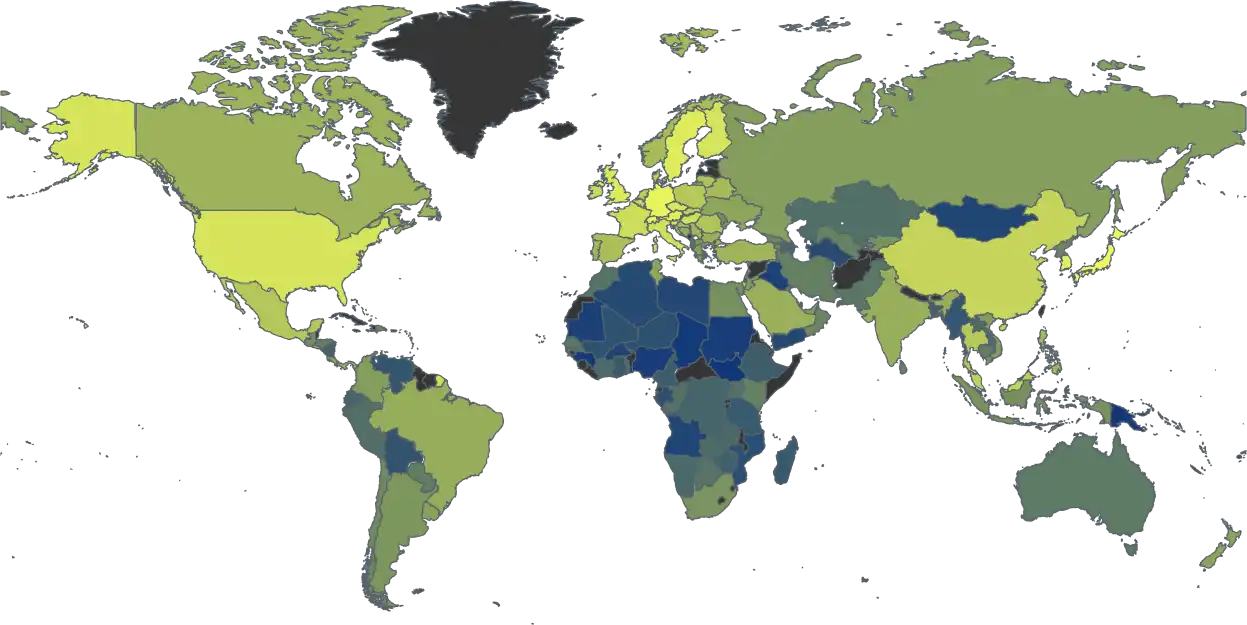
The Economic Complexity Index, or ECI, is a measure of an economy's capacity which can be inferred from data connecting locations to the activities that are present in them. The Economic Complexity Index has been shown to predict important macroeconomic outcomes, including a country's level of income^14,15,economic growth^14,15, income inequality¹⁶,and greenhouse gas emissions.^17,18, It has also been estimated using diverse data sources, such as trade data^14,15, employment data²⁵, stock market data²⁶,and patent data²⁷.

The Product Complexity Index, or PCI, is a measure of the complexity required to produce a product or engage in an economic activity. The Product Complexity Index is correlated with the spatial concentration of economic activities²⁸.

Imagine being asked to grade a multiple choice exam in a language you have never heard. To help you grade the exam, the teacher gives you an answer key, but also informs you that you need to award more points to challenging questions. The teacher doesn't have a key for that, so you need to infer the difficulty of questions directly from the student's answers?

One way to start is to look at how many students answered each question correctly. Easy questions were probably answered correctly by most students, while difficult questions were probably answered correctly by only a few students. Yet, some students may be guessing their answers, so a correct answer means more if it is coming from a student that answered most questions correctly.

This thought experiment should give you the basic intuition behind economic complexity. Now, think that instead of students you have economies (e.g. countries, cities, regions), and instead of questions you have economic activities (products, industries, technologies). Economic complexity is the idea that you can infer “how good of a student” an economy is by looking at the activities that it is able to develop successfully, and by looking at the other places where those activities are present.

The problem of estimating economic complexity is the problem of estimating both, the complexity of locations (e.g. countries, cities, regions) and that of the activities present in them (e.g. products, industries, technologies). The general idea is that the activities present, produced, or exported from a location, carry information about the complexity of that location, while the locations where an activity is present carry information about the complexity required to perform an activity. For instance, we can say that cities like San Francisco, Boston, and New York, are complex, because they are home to complex activities. Similarly, we can say that an activity like biotech or aerospace is complex, if it is found mostly in complex economies, like those of Boston and San Francisco.

This circular argument can be translated into a general set of equations that can be used to estimate the complexity of economies.

Formally, let the complexity K of a location c (e.g. country or city) be \(K_{c}\) and the complexity K of an activity p (e.g. product or industry) be \(K_{p}\) . Also, let \(M_{cp}\) be a matrix summarizing the activities (p) present in location (c). Usually,, \(M_{cp}\) is defined as \(M_{cp} = 1\) when a location's output in an activity is larger than what is expected for a location ofthe same size and an activity with the same total output. This can be done using an indicator such as a location's Revealed Comparative Advantage (RCA) or Location Quotient (LQ).

That is, we can define

Where

and

Following this notation, the general assumption made by metrics of economic complexity is that:

(i) The complexity of a location (\(K_{c}\)) is a function (f) of the complexity (\(K_{p}\)) of the activities present in it (\(M_{cp}\), ), and

(ii) The complexity of an activity (\(K_{p}\)) is a function (g) of the complexity (\(K_{c}\)) of the places where that activity is present (\(M_{cp}\)).

This circular logic is equivalent to the following mathematical map.²⁸

Where f and g are functions to be determined.

These mappings imply that measures of the complexity of economies, or of economic activities, are solutions to self-consistent equations of the form:

Which in many occasions can be reduced—or approximated by—a linear equation of the form:

These equations imply that metrics of the complexity of economies, or of the activities present in them, are respectively, eigenvectors of matrices connecting related countries (\(M_{cc'}\)) or related products (\(M_{pp'}\)) (e.g. the Product Space). We note that the first set of equations provide a more generalfamily of functions that includes functions that cannot be reduced to the linear forms, yet, they can provide results that are similar to those obtained by linear equations..

These equations also tell us that measures of complexity are relative measures, since the complexity of a location or an activity can change because of changes in the entries for other locations or activities (other rows or columns in the \(R_{cp}\) or \(M_{cp}\) matrix).

Using the above framework, we define the Economic Complexity Index of a location, or ECI, as the average of the Product Complexity Index, or PCI, of the activities present in it. Similarly, we define the Product Complexity Index of an activity, or PCI, as the average Economic Complexity Index, or ECI, of the locations where that activity is present. That is, we define the complexity of a location as the average complexity of its activities, and the complexity of an activity, as the average complexity of the places where that activity is present. Formally, the ECI formula is the solution to the system of equations:

Which, upon putting the second equation in the first one, is equivalent to diagonalizing the following matrix:

Here \(M_c=\sum_p M_{cp}\) is the number of activities (or diversity) of a location and \(M_p=\sum_c M_{cp}\) is the ubiquity of an activity (number of locations where it is present).

Since Economic Complexity is a relative metric, the results are usually normalized using a Z-transform. That is:

Where \(\tilde{K_{c}}\) is the average of \(K_{c}\) and \(\sigma(K_c)\) is the standard deviation of \(K_{c}\).

Since subnational level data varies in terms of the units of observation (provinces, municipalities, etc.), we combine PCIs calculated using international trade data, with presence absence matrices characterizing local data.

Formally, we define subnational ECIs as:

Here, we define \(M_{cp}\) using the following modified version of RCA:

That is, we compare the share of an activity in a local unit (e.g. region, province), with the share of that activity in the world. This is to avoid having the most developed regions in a country appear to have comparative advantage in every product, and also, to make the ECI values obtained for subnational regions comparable with those of countries in the international datasets.

During the last decades a number of studies have documented relationships between economic complexity and important social and macroeconomic outcomes.

The first string of studies focused on the relationship between economic complexity and economic growth. The paper that introduced the idea of economic complexity¹⁴,showed that economies with higher economic complexity, per unit of GDP per capita, grew faster. This finding was later confirmed and expanded in a subsequent book (The Atlas of Economic Complexity) and in various papers using international and subnational level data^29–32. On average, scholars find that an increase of one standard deviation in economic complexity, at the same level of GDP per capita, is associated with an increase in annualized growth of between 4% to 7%. This is a strong effect, but it is important to keep in mind that an increase of one standard deviation in ECI is an extremely large effect (since ECI values, which are normalized, range usually between -2 and 2).

More recently, people studying economic complexity have turned their attention to other topics, such as income inequality and environmental sustainability.

In recent years we have learned that countries with higher levels of economic complexity tend to experience lower levels of income inequality^16,33,and also, to produce a comparatively lower number of emissions^17,18.

Together, the ability of economic complexity to predict economic growth, inequality, and lowered emissions, make it an interesting policy target for countries looking to foster inclusive development.